Pulse-level circuit simulation¶

Modelling quantum hardware with Processor¶

Based on the open system solver, Processor in the qutip.qip module simulates quantum circuits at the level of time evolution. One can consider the processor as a simulator of a quantum device, on which the quantum circuit is to be implemented.

The procedure is illustrated in the figure below. It first compiles circuit into a Hamiltonian model, adds noisy dynamics and then uses the QuTiP open time evolution solvers to simulation the evolution.

Like a real quantum device, the processor is determined by a list of Hamiltonians, i.e. the control pulses driving the evolution. Given the intensity of the control pulses and the corresponding time slices for each pulse, the evolution is then computed. A control pulse is characterized by Pulse, consisting of the control Hamiltonian, the targets qubit, the pulse coefficients and the time sequence. We can either use the coefficients as a step function or with cubic spline. For step function, tlist specifies the start and the end of each pulse and thus is one element longer the coeffs. One example of defining the control pulse coefficients and the time array is as follows:

import numpy as np
from qutip import sigmaz
from qutip.qip.device import Processor

processor = Processor(2)
processor.add_control(sigmaz(), cyclic_permutation=True)  # sigmaz for all qubits
processor.pulses[0].coeffs = np.array([[1.0, 1.5, 2.0], [1.8, 1.3, 0.8]])
processor.pulses[0].tlist = np.array([0.1, 0.2, 0.4, 0.5])

It defines a \(\sigma_z\) operator on both qubits and a pulse that acts on the first qubit. An equivalent approach is using the add_pulse method.

from qutip.qip.pulse import Pulse

processor = Processor(2)
coeff=np.array([0.1, 0.2, 0.4, 0.5])
tlist=np.array([[1.0, 1.5, 2.0], [1.8, 1.3, 0.8]])
pulse = Pulse(sigmaz(), targets=0, coeff=coeff, tlist=tlist)
processor.add_pulse(pulse)

One can also use choose the pulse_mode attribute of Processor between "discrete" and "continuous".

The above example shows the framework and the most essential part of the simulator’s API. So far, it looks like just a wrapper for the open system solvers. However, based on this, we can implement different physical realizations. They differ mainly in how to find the control pulse for a quantum circuit, which gives birth to different sub-classes:

In general, there are two ways to find the control pulses. The first one, ModelProcessor, is more experiment-oriented and based on physical models. A universal set of gates is defined in the processor as well as the pulse implementing them in this particular physical model. This is usually the case where control pulses realizing those gates are well known and can be concatenated to realize the whole quantum circuits. Two realizations have already been implemented: the spin chain and the Cavity QED model for quantum computing. In those models, the driving Hamiltonians are predefined. Another approach, based on the optimal control module in QuTiP (see Quantum Optimal Control), is called OptPulseProcessor. In this subclass, one only defines the available Hamiltonians in their system. The processor then uses algorithms to find the optimal control pulses that realize the desired unitary evolution.

Despite this difference, the logic behind all processors is the same:

• One defines a processor by a list of available Hamiltonians and, as explained later, hardware-dependent noise. In model based processors, the Hamiltonians are predefined and one only needs to give the device parameters like frequency and interaction strength.

• The control pulse coefficients and time slices are either specified by the user or calculated by the method load_circuit, which takes a QubitCircuit and find the control pulse for this evolution.

• The processor calculates the evolution using the QuTiP solvers. Collapse operators can be added to simulate decoherence. The method run_state returns a object qutip.solver.Result.

It is also possible to calculate the evolution analytically with matrix exponentiation by setting analytical=True. A list of the matrices representing the gates is returned just like for propagators. However, this does not consider the collapse operators or other noise. As the system size gets larger, this approach will become very inefficient.

In the following we describe the predefined subclasses for Processor:

SpinChain

LinearSpinChain and CircularSpinChain are quantum computing models base on the spin chain realization. The control Hamiltonians are \(\sigma_x\), \(\sigma_z\) and \(\sigma_x \sigma_x + \sigma_y \sigma_y\). This processor will first decompose the gate into the universal gate set with ISWAP or SQRTISWAP as two-qubit gates, resolve them into quantum gates of adjacent qubits and then calculate the pulse coefficients.

An example of simulating a simple circuit is shown below:

from qutip import basis
from qutip.qip.circuit import QubitCircuit
from qutip.qip.device import LinearSpinChain

qc = QubitCircuit(2)
qc.add_gate("X", targets=0)
qc.add_gate("X", targets=1)
processor = LinearSpinChain(2)
processor.load_circuit(qc)
result = processor.run_state(basis([2,2], [0,0]))
print(result.states[-1].tidyup(1.0e-6))

Quantum object: dims = [[2, 2], [1, 1]], shape = (4, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 0.]
[-1.]]

We can also visualize the pulses implementing this circuit:

from qutip import basis
from qutip.qip.circuit import QubitCircuit
from qutip.qip.device import LinearSpinChain

qc = QubitCircuit(2)
qc.add_gate("X", targets=0)
qc.add_gate("X", targets=1)
processor = LinearSpinChain(2)
processor.load_circuit(qc)
fig, axis = processor.plot_pulses()
fig.show()

(png, hires.png, pdf)

DispersiveCavityQED

Same as above, DispersiveCavityQED is a simulator based on Cavity Quantum Electrodynamics. The workflow is similar to the one for the spin chain, except that the component systems are a multi-level cavity and a qubits system. The control Hamiltonians are the single-qubit rotation together with the qubits-cavity interaction \(a^{\dagger} \sigma^{-} + a \sigma^{+}\). The device parameters including the cavity frequency, qubits frequency, detuning and interaction strength etc.

OptPulseProcessor

The OptPulseProcessor uses the function in optimize_pulse_unitary in the optimal control module to find the control pulses. The Hamiltonian includes a drift part and a control part and only the control part will be optimized. The unitary evolution follows

To let it find the optimal pulses, we need to give the parameters for optimize_pulse_unitary as keyword arguments to load_circuit. Usually, the minimal requirements are the evolution time evo_time and the number of time slices num_tslots for each gate. Other parameters can also be given in the keyword arguments. For available choices, see optimize_pulse_unitary. It is also possible to specify different parameters for different gates, as shown in the following example:

from qutip.qip.device import OptPulseProcessor
from qutip.operators import sigmaz, sigmax, sigmay
from qutip.tensor import tensor

# Same parameter for all the gates
qc = QubitCircuit(N=1)
qc.add_gate("SNOT", 0)

num_tslots = 10
evo_time = 10
processor = OptPulseProcessor(N=1, drift=sigmaz())
processor.add_control(sigmax())
# num_tslots and evo_time are two keyword arguments
tlist, coeffs = processor.load_circuit(
qc, num_tslots=num_tslots, evo_time=evo_time)

# Different parameters for different gates
qc = QubitCircuit(N=2)
qc.add_gate("SNOT", 0)
qc.add_gate("SWAP", targets=[0, 1])
qc.add_gate('CNOT', controls=1, targets=[0])

processor = OptPulseProcessor(N=2, drift=tensor([sigmaz()]*2))
processor.add_control(sigmax(), cyclic_permutation=True)
processor.add_control(sigmay(), cyclic_permutation=True)
processor.add_control(tensor([sigmay(), sigmay()]))

setting_args = {"SNOT": {"num_tslots": 10, "evo_time": 1},
                "SWAP": {"num_tslots": 30, "evo_time": 3},
                "CNOT": {"num_tslots": 30, "evo_time": 3}}

tlist, coeffs = processor.load_circuit(
                qc, setting_args=setting_args, merge_gates=False)

Compiler and scheduler¶

In order to simulate quantum circuits at the level of time evolution. We need to first compile the circuit into the Hamiltonian model, i.e. the control pulses. Hence each Processor has a corresponding GateCompiler class. The compiler takes a QubitCircuit and returns the compiled tlist and coeffs. It is called implicitly when calling the method run_state.

from qutip.qip.compiler import SpinChainCompiler
qc = QubitCircuit(2)
qc.add_gate("X", targets=0)
qc.add_gate("X", targets=1)

processor = LinearSpinChain(2)
compiler = SpinChainCompiler(
    2, params=processor.params, pulse_dict=processor.pulse_dict)
resolved_qc = qc.resolve_gates(["RX", "RZ", "ISWAP"])
tlists, coeffs = compiler.compile(resolved_qc)
print(tlists)
print(coeffs)

Output

[array([0., 1.]), array([0., 1., 2.]), None, None, None]
[array([1.57079633]), array([0.        , 1.57079633]), None, None, None]

Here we first use resolve_gates to decompose the X gate to its natural gate on Spin Chain model, the rotation over X-axis. We pass the hardware parameters of the SpinChain ` model, processor.params, as well as a map between the pulse name and pulse index pulse_dict to the compiler. The later one allows one to address the pulse more conveniently in the compiler.

The compiler returns a list of tlist and coeff, corresponding to each pulse. The first pulse starts from t=0 and ends at t=1, with the strengh \(\pi/2\). The second one is turned on from t=1 to t=2 with the same strength. The compiled pulse here is different from what is shown in the plot in the previous subsection because the scheduler is turned off by default.

The scheduler is implemented in the class Scheduler, based on the idea of https://doi.org/10.1117/12.666419. It schedules the order of quantum gates and instructions for the shortest execution time. It works not only for quantum gates but also for pulse implementation of gates (Instruction) with varying pulse duration.

The scheduler first generates a quantum gates dependency graph, containing information about which gates have to be executed before some other gates. The graph preserves the mobility of the gates, i.e. commuting gates are not dependent on each other, even if they use the same qubits. Next, it computes the longest distance of each node to the start and end nodes. The distance for each dependency arrow is defined by the execution time of the instruction (By default, it is 1 for all gates). This is used as a priority measure in the next step. The gate with a longer distance to the end node and a shorter distance to the start node has higher priority. In the last step, it uses a list-schedule algorithm with hardware constraint and priority and returns a list of cycles for gates/instructions. Since the algorithm is heuristics, sometimes it does not find the optimal solution. Hence, we offer an option that randomly shuffles the commuting gates and repeats the scheduling a few times to get a better result.

from qutip.qip.circuit import QubitCircuit
from qutip.qip.compiler import Scheduler
circuit = QubitCircuit(7)
circuit.add_gate("SNOT", 3)  # gate0
circuit.add_gate("CZ", 5, 3)  # gate1
circuit.add_gate("CZ", 4, 3)  # gate2
circuit.add_gate("CZ", 2, 3)  # gate3
circuit.add_gate("CZ", 6, 5)  # gate4
circuit.add_gate("CZ", 2, 6)  # gate5
circuit.add_gate("ISWAP", [0, 2])  # gate6
scheduler = Scheduler("ASAP")
result = scheduler.schedule(circuit, gates_schedule=True)
print(result)

Output

[0, 1, 3, 2, 2, 3, 4]

The result shows the scheduling order of each gate in the original circuit.

For pulse schedule, or scheduling gates with different duration, one will need to wrap the qutip.qip.circuit.Gate object with qutip.qip.compiler.instruction object, with a parameter duration. The result will then be the start time of each instruction.

Noise Simulation¶

In the common way of QIP simulation, where evolution is carried out by gate matrix product, the noise is usually simulated with bit flipping and sign flipping errors. The typical approaches are either applying bit/sign flipping gate probabilistically or applying Kraus operators representing different noisy channels (e.g. amplitude damping, dephasing) after each unitary gate evolution. In the case of a single qubit, they have the same effect and the parameters in the Kraus operators are exactly the probability of a flipping error happens during the gate operation time.

Since the processor simulates the state evolution at the level of the driving Hamiltonian, there is no way to apply an error operator to the continuous-time evolution. Instead, the error is added to the pulses (coherent control error) or the collapse operators (Lindblad error) contributing to the evolution. Mathematically, this is no different from adding error channel probabilistically (it is actually how qutip.mcsolve works internally). The collapse operator for single-qubit amplitude damping and dephasing are exactly the destroying operator and the sign-flipping operator. One just needs to choose the correct coefficients for them to simulate the noise, e.g. the relaxation time T1 and dephasing time T2. Because it is based on the open system evolution instead of abstract operators, this simulation is closer to the physical implementation and requires less pre-analysis of the system.

Compared to the approach of Kraus operators, this way of simulating noise is more computationally expensive. If you only want to simulate the decoherence of single-qubit relaxation and the relaxation time is much longer than the gate duration, there is no need to go through all the calculations. However, this simulator is closer to the real experiment and, therefore, more convenient in some cases, such as when coherent noise or correlated noise exist. For instance, a pulse on one qubit might affect the neighbouring qubits, the evolution is still unitary but the gate fidelity will decrease. It is not always easy or even possible to define a noisy gate matrix. In our simulator, it can be done by defining a ControlAmpNoise (Control Amplitude Noise).

In the simulation, noise can be added to the processor at different levels:

• The decoherence time T1 and T2 can be defined for the processor or for each qubit. When calculating the evolution, the corresponding collapse operators will be added automatically to the solver.

• The noise of the physical parameters (e.g. detuned frequency) can be simulated by changing the parameters in the model, e.g. laser frequency in cavity QED. (This can only be time-independent since QuTiP open system solver only allows varying coefficients, not varying Hamiltonian operators.)

• The noise of the pulse intensity can be simulated by modifying the coefficients of the Hamiltonian operators or even adding new Hamiltonians.

To add noise to a processor, one needs to first define a noise object Noise. The simplest relaxation noise can be defined directly in the processor with relaxation time. Other pre-defined noise can be found as subclasses of Noise. We can add noise to the simulator with the method add_noise.

Below, we show two examples.

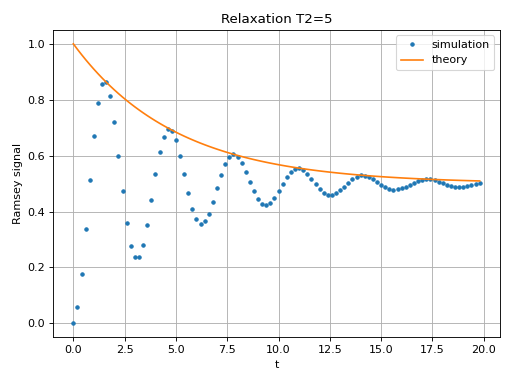
The first example is a processor with one qubit under rotation around the z-axis and relaxation time \(T_2=5\). We measure the population of the \(\left| + \right\rangle\) state and observe the Ramsey signal:

import numpy as np
import matplotlib.pyplot as plt
from qutip import sigmaz, destroy, basis
from qutip.qip.device import Processor
from qutip.qip.operations import snot

a = destroy(2)
Hadamard = snot()
plus_state = (basis(2,1) + basis(2,0)).unit()
tlist = np.arange(0.00, 20.2, 0.2)

T2 = 5
processor = Processor(1, t2=T2)
processor.add_control(sigmaz())
processor.pulses[0].coeff = np.ones(len(tlist))
processor.pulses[0].tlist = tlist
result = processor.run_state(
    plus_state, e_ops=[a.dag()*a, Hadamard*a.dag()*a*Hadamard])

fig, ax = plt.subplots()
# detail about length of tlist needs to be fixed
ax.plot(tlist[:-1], result.expect[1][:-1], '.', label="simulation")
ax.plot(tlist[:-1], np.exp(-1./T2*tlist[:-1])*0.5 + 0.5, label="theory")
ax.set_xlabel("t")
ax.set_ylabel("Ramsey signal")
ax.legend()
ax.set_title("Relaxation T2=5")
ax.grid()
fig.tight_layout()
fig.show()

(png, hires.png, pdf)

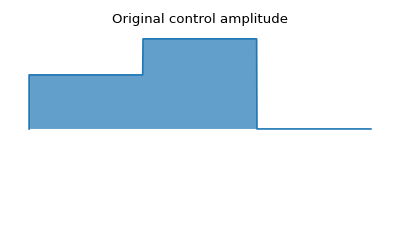
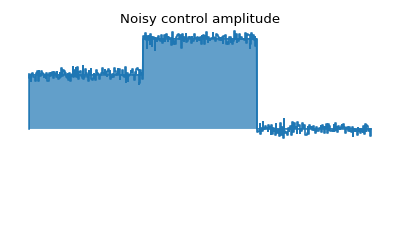
The second example demonstrates a biased Gaussian noise on the pulse amplitude. For visualization purposes, we plot the noisy pulse intensity instead of the state fidelity. The three pulses can, for example, be a zyz-decomposition of an arbitrary single-qubit gate:

import numpy as np
import matplotlib.pyplot as plt
from qutip import sigmaz, sigmay
from qutip.qip.device import Processor
from qutip.qip.noise import RandomNoise

# add control Hamiltonians
processor = Processor(N=1)
processor.add_control(sigmaz(), targets=0)

# define pulse coefficients and tlist for all pulses
processor.pulses[0].coeff = np.array([0.3, 0.5, 0. ])
processor.set_all_tlist(np.array([0., np.pi/2., 2*np.pi/2, 3*np.pi/2]))

# define noise, loc and scale are keyword arguments for np.random.normal
gaussnoise = RandomNoise(
            dt=0.01, rand_gen=np.random.normal, loc=0.00, scale=0.02)
processor.add_noise(gaussnoise)

# Plot the ideal pulse
fig1, axis1 = processor.plot_pulses(title="Original control amplitude", figsize=(5,3))

# Plot the noisy pulse
qobjevo, _ = processor.get_qobjevo(noisy=True)
noisy_coeff = qobjevo.to_list()[1][1] + qobjevo.to_list()[2][1]
fig2, axis2 = processor.plot_pulses(title="Noisy control amplitude", figsize=(5,3))
axis2[0].step(qobjevo.tlist, noisy_coeff)

(png, hires.png, pdf)¶

(png, hires.png, pdf)¶

Customize the simulator¶

The number of predefined physical models and compilers are limited. However, it is designed for easy customization and one can easily build customized model and compiling routines. For guide and examples, please refer to the tutorial notebooks at https://qutip.org/tutorials.html

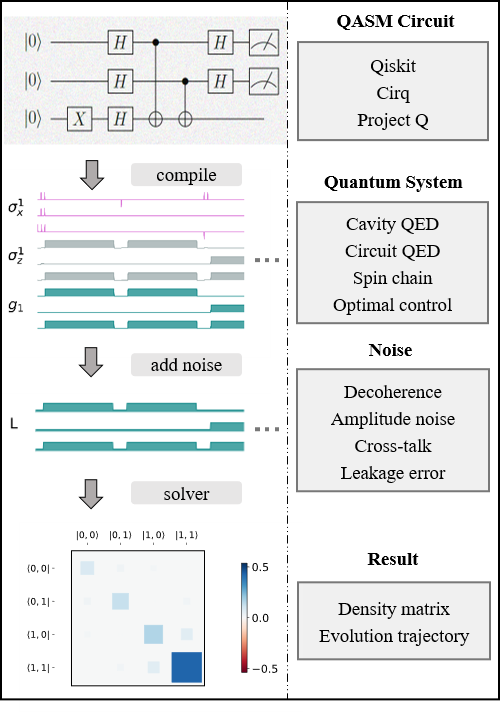
The workflow of the simulator¶

The following plot demonstrates the workflow of the simulator.

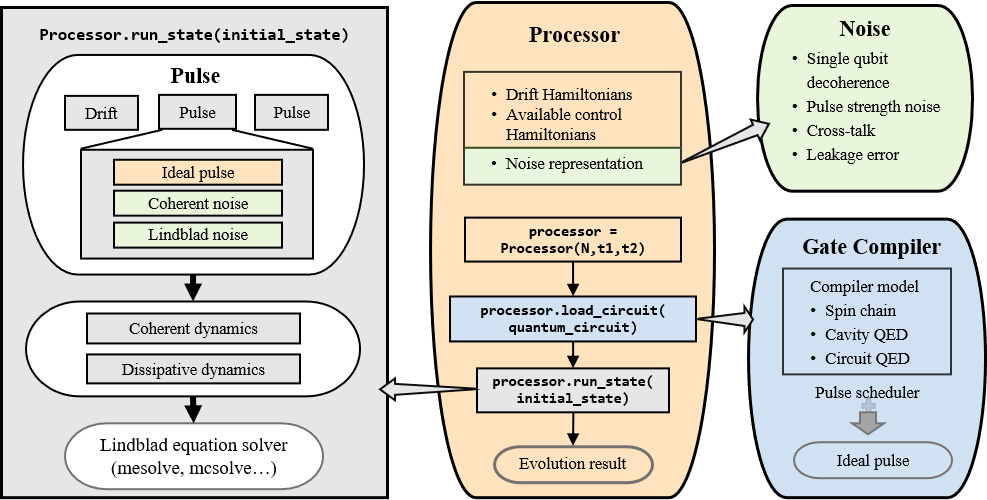
The core of the simulator is Processor, which characterizes the quantum hardware of interest, containing the information such as the non-controllable drift Hamiltonian and the control Hamiltonian. Apart from the ideal system representing the qubits, one can also define hardware-dependent or pulse-dependent noise in Noise. It describes how noisy terms such as imperfect control and decoherence can be added once the ideal control pulse is defined. When loading a quantum circuit, a GateCompiler compiles the circuit into a sequence of control pulse signals and schedule the pulse for parallel execution. For each control Hamiltonian, a Pulse instance is created that including the ideal evolution and associated noise. They will then be sent to the QuTiP solvers for the computation.